Consideriamo una generica reazione chimica:
A + B -> C + D
Abbiamo visto nella unità didattica precedente come la velocità di questa reazione sia valutabile dalla legge cinetica che in questo caso (supponendo un passaggio unico di reazione) può essere scritta come:
V d = kd [A] [B]
Man mano che la reazione procede la concentrazione dei reagenti diminuisce per cui anche la velocità di questa reazione rallenta.
Durante la reazione di formano dei prodotti per cui noi dobbiamo pensare anche ad una possibile reazione inversa a quella che abbiamo descritto di sopra:
C + D -> A + B
Anche questa reazione avrà una certa velocità, che inizialmente sarà (dato che le concentrazioni di C e D sono basse) lenta, ma con il passare del tempo, causa la produzione di C e di D ed il loro aumento di concentrazione andrà in crescendo.
La velocità di questa reazione inversa sarà espressa dalla seguente legge cinetica:
V i = ki [C] [D]
Poichè V d tende a diminuire e V i tende ad aumentare arriveremo ad una condizione in cui:
V d = V i per cui kd [A] [B] = ki [C] [D]
Si tratta di una condizione di equilibrio dinamico, ossia una situazione in cui reagenti si trasformano in prodotti e prodotti si trasformano in reagenti con la stessa velocità.
In questa condizione le concentrazioni dei reagenti e prodotti si mantengono in pratica costanti (attenzione costanti non vuol dire che le concentrazioni dei reagenti e prodotti sono uguali ma solo che non variano nel tempo).
Poichè all’equilibrio
kd [A] [B] = ki [C] [D]
possiamo dire che kd / ki = [C] [D]/[A] [B]
Ma il rapporto tra le due costanti kd / ki è a sua volta una costante che chiameremo costante di equilibrio ke da cui
ke = [C] [D]/[A] [B]
Nell’unità didattica precedente avevamo visto come le costanti delle equazioni cinetiche erano costanti a temperatura costante, quindi anche per la ke che deriva da un rapporto di due di questi costanti varrà la stessa regola.
Se la reazione chimica presentasse dei coefficienti stechiometrici ad esempio:
aA + bB -> cC + dD rifacendo lo stesso ragionamento troveremo
(1) Ke = [C]c [D]d/[A]a [B]b
l’espressione (1) rappresenta la cosiddetta legge delle masse che può essere espressa nel seguente modo.
“In una reazione chimica all’equilibrio a temperatura costante il rapporto tra il prodotto delle concentrazioni dei prodotti ed il rapporto delle concentrazione dei reagenti con tutti i termini elevati ai rispettivi coefficienti stechiometrici è costante”.
Facciamo un esempio pratico considerando la seguente reazione
N2(g) + 3H2 (g) <-> 2NH3(g) (g) = gassoso
Ke= [NH3]2/[N2][H2]3
L’espressione della legge delle masse non è altro che una applicazione di un principio più vasto denominato PRINCIPIO DI LECHATELIER il quale si può esprimere nei seguenti termini:
“In un sistema in condizione di equilibrio se si interviene dall’esterno perturbando la condizione di equilibrio il sistema reagirà cercando di ripristinare la condizione preesistente”.
Vediamo un esempio di applicazione del principio sopra esposto, torniamo alla nostra reazione di sintesi dell’ammoniaca
N2(g) + 3H2 (g) <-> 2NH3(g)
Se questa reazione ha raggiunto l’equilibrio cosa succede se dall’esterno aggiungo altro azoto (N2) o altro idrogeno (H2), in altre parole se aggiungo dei reagenti?
Secondo il principio di Lechatelier il sistema cercherà di neutralizzare tale operazione e per farlo dovrà produrre altra ammoniaca (NH3), in questo modo consuma i reagenti aggiunti.
A tale risultato ci saremmo arrivati anche con la legge delle masse, infatti dato che:
Ke= [NH3]2/[N2][H2]3
se aumentiamo i termini al denominatore (reagenti) il valore si manterrà costante unicamente aumentando il numeratore (prodotti).
Quindi in una reazione chimica all’equilibrio potremo aumentare la resa in prodotti aggiungendo dei reagenti (spostamento a destra della reazione).
Il risultato diametralmente opposto ovviamente si sarebbe ottenuto se avessimo aggiunto dei prodotti (in questo caso l’equilibrio chimico viene spostato verso sinistra).
Seguendo analogo ragionamento dovremmo capire come sia possibile favorire una reazione chimica anche sottraendo i prodotti man mano che si formano, in questo caso, infatti, il sistema reagirà cercando di riformare i prodotti che abbiamo sottratto.
Le osservazioni che abbiamo fatto sono molto importanti a livello industriale, aumenti della resa di produzione portano ad ovvi vantaggi economici.
Appare a questo punto chiaro come mai, ad esempio, nella sintesi dell’ammoniaca si opera con eccessi di reagenti (idrogeno e azoto) ed asportando il prodotto mano mano che esso si forma.
Ma non è solo attraverso la concentrazione dei reagenti e prodotti che possiamo spostare a destra o sinistra gli equilibri chimici, altri parametri importanti sono:
- Pressione
- Temperatura
PRESSIONE
La pressione consente lo spostamento degli equilibri chimici in cui ci siano delle specie chimiche in fase gassosa.
Sono infatti le molecole gassose che sono associate alla pressione dei gas stessi.
Torniamo alla nostra reazione di esempio
1N2(g) + 3H2 (g) <-> 2NH3(g)
Il numero di molecole di gas nei reagenti sono 4 (1+3)
Il numero di molecole di gas nei prodotti sono 2
Spostando l’equilibrio verso destra il numero di molecole di gas diminuiscono e quindi diminuisce la pressione, viceversa ovviamente se l’equilibrio si sposta verso sinistra.
Come reagirà il nostro equilibrio ad un aumento forzato di pressione?
Secondo il principio di Lechatelier diminuendola ossia spostando l’equilibrio in modo di ridurre il numero di molecole gassose, in altre parole verso destra.
Non per niente gli impianti di produzione dell’ammoniaca lavorano ad alte pressioni.
In caso in cui nelle reazioni non comparissero specie gassose o non ci fosse variazione del numero di molecole gassose ovviamente la pressione non influenzerebbe l’equilibrio.
TEMPERATURA
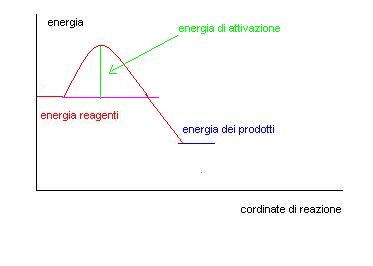
Nell’unità didattica precedente abbiamo visto dei grafici di questo tipo
Soffermiamoci ad analizzare lo stato iniziale e quello finale.
In questo caso troviamo che l’energia dei reagenti (inizio trasformazione)
è maggiore dell’energia dei prodotti (fine trasformazione).
Durante questa trasformazione il nostro sistema ha perso dell’energia, ma poichè come sappiamo l’energia non si crea e non si distrugge dove è finita questa energia mancante?
Ovviamente il nostro sistema deve avere ceduto energia all’ambiente.
La forma di energia che più frequentemente viene scambiata tra ambiente e sistema è il calore.
Possiamo quindi immaginare che la reazione del grafico sopra riportato ceda del calore all’ambiente, questo tipo di reazioni vengono denominate ESOTERMICHE.
Se indichiamo con Q il calore scambiato possiamo scrivere una reazione generica esotermica come:
A + B -> C + D + Q (calore)
(un modo per ricordarsi la posizione di Q è ISO = 3 lettere = PIU,)
Nel caso in cui siano i prodotti ad avere maggiore energia dei reagenti il discorso va ovviamente ribaltato, in questo caso è il sistema ad “acquistare” energia dall’ambiente (che si raffredda) provocando delle reazioni denominate ENDOTERMICHE
Se indichiamo con Q il calore scambiato possiamo scrivere una reazione generica endotermica come:
A + B -> C + D – Q (calore)
(un modo per ricordarsi la posizione di Q è ENDO = 4 lettere = MENO,)
NB si può ovviamente scrivere, cambiando si segno, anche
A + B + Q (calore) -> C + D
Ci sono poi reazioni in cui reagenti e prodotti hanno la stessa energia ed in questo caso si parla di reazioni ISOTERMICHE.
Le reazioni esotermiche e quelle endotermiche sono influenzate dalla temperatura.
Se consideriamo il calore (Q) come se fosse un reagente e consideriamo il principio di Le Chetelier è facile capire come questo tipo di reazioni rispondano alle variazioni di temperatura.
Se scaldiamo il sistema cercherà di raffreddare per cui favoriremo le reazioni endotermiche
A + B -> C + D – Q (calore) = A + B + Q (calore) -> C + D
(e come se aggiungessimo Q a sinistra o cavassimo Q da destra) l’equilibrio si sposta verso destra.
Se raffreddiamo il sistema cercherà di produrre calore per cui favoriremo le reazioni esotermiche
A + B -> C + D + Q (calore)
Ovviamente le reazioni isotermiche non saranno influenzate da variazioni di temperatura.
Gli equilibri eterogenei
Quando tutte le sostanze (reagenti e prodotti) che partecipano all’equilibrio sono nello stesso stato fisico (ad esempio tutti gas o tutti liquidi) l’equilibrio si definisce omogeneo.
Se questa condizione non si verifica (basta che un componente, reagente o prodotto, sia in uno stato fisico diverso) l’equilibrio si definisce eterogeneo.
Un esempio di equilibrio eterogeneo è il seguente
CaCO3(s) <–> CaO(s) +CO2(g)
SPONTANEITA’ DELLE REAZIONI
Fino ad ora abbiamo eseguito delle considerazioni unicamente riferendoci agli aspetti cinetici dei processi chimici.
Abbiamo visto che in termini cinetici una reazione può essere lenta o veloce e diversi fattori possono influenzare i tempi che essa necessita per avvenire.
Non dobbiamo però confondere la velocità di una reazione con la sua spontaneità.
Facciamo un esempio se io osservo un pezzo di ferro per due giorni consecutivi non vedo nessuna trasformazione, ma se lo guardo dopo un anno vedo che si è formata della ruggine.
Per formare della ruggine non è stato necessario fornire dell’energia al pezzo di ferro, abbiamo quindi a che fare con un processo spontaneo, ma relativamente lento.
Se dovessi decomporre l’H2O in idrogeno ed Ossigeno dovrei per forza fornire dell’energia.
Questa trasformazione non è quindi spontanea, ma fornendo energia sufficiente può avvenire anche rapidamente.
Vediamo le reazioni dei due processi indicati:
2Fe + 3O2 <-> 2Fe2O3 (i)
2H2O <-> 2H2 + O2 (ii)
Come possiamo stabilire a priori che la prima delle due reazioni è spontanea mentre la seconda non lo è ?
Per rispondere a questa domanda dobbiamo prendere in considerazioni alcune variabili particolari chiamate variabili Termodinamiche.
Lo studio termodinamico dei processi chimici è abbastanza complesso per cui noi ci limiteremo ad una valutazione estremamente sintetica dell’argomento.
Supponiamo di avere una pallina su di un pendio scosceso, se la pallina è libera di muoversi possiamo prevedere che essa spontaneamente rotoli verso il basso.
In pratica la pallina si muove spontaneamente da una situazione in cui ha un massimo di energia (cima del pendio) verso una situazione in cui la sua energia è minima (fondo del pendio).
Teoricamente durante questo rotolamento la pallina può avere percorso infiniti tipi di tragitti, ma questo a noi non interessa, quello che conta sono solo l’istante iniziale (pallina in cima al pendio) e quello finale (pallina in fondo al pendio).
Le variabili termodinamiche che prenderemo in considerazione hanno tutte una caratteristica particolare, infatti, esse dipendono unicamente dalla variazione tra stato finale ed iniziale della trasformazione è sono indipendenti dal percorso che la trasformazione ha eseguito.
Per fare una analogia le variabili termodinamiche sono come l’indicazione di un dislivello di una pista di sci (ad esempio 200 m) che non considera però la difficoltà della pista stessa.
Lo stesso dislivello infatti può essere disceso su di una pista nera o azzurra con dispendio di energia ben diverso.
LE GRANDEZZE TERMODINAMICHE CHE DIPENDONO UNICAMENTE DALLA DIFFERENZA TRA STATO INIZIALE E FINALE PRENDONO IL NOME DI FUNZIONI DI STATO.
Una delle variabili che viene abbiamo preso già in considerazione in una trasformazione chimica è il calore.
Il calore in condizioni normali non è una funzione di stato, ma lo diventa in condizioni particolari.
Ad esempio se la trasformazione avviene a pressione costante il calore scambiato diventa una funzione di stato (indipendente dal cammino seguito dalla trasformazione stessa).
Questo ci è molto comodo anche tenendo in considerazione il fatto che molte reazioni si possono far avvenire a pressione costante (ad esempio quella atmosferica).
Il calore scambiato a pressione costante ha quindi delle caratteristiche particolari tanto da essere chiamato come ENTALPIA.
La variazione di entalpia (simbolo ΔH) è quindi una funzione di stato è rappresenta il calore scambiato a pressione costante.
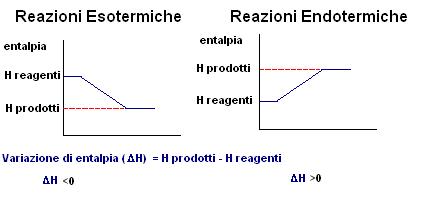
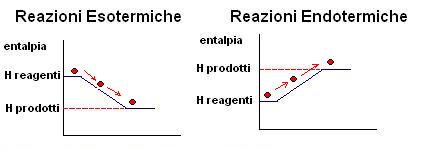
Come sappiamo il calore non è altro che una forma di energia per cui possiamo rappresentare i grafici che abbiamo già visto in precedenza (Energia in funzione dello svolgimento della reazione) come Entalpia in funzione dello svolgimento della reazione.
Ragionando in questi termini avremo:
Le reazioni esotermiche hanno quindi un DH<0, mentre le reazioni endotermiche hanno un DH>0.
Abbiamo visto come nelle reazioni esotermiche sia il il sistema a cedere energia all’ambiente, in pratica cioè il sistema evolve da uno stato di energia massima ad uno di energia minima trasferendo la quota di energia persa all’ambiente.
Una reazione esotermica può essere quindi vista alla stregua di una pallina che scende da un pendio.
A questo punto sembrerebbe ovvio che siano le reazioni esotermiche quelle spontanee, mentre quelle endotermiche potranno avvenire solo se forniamo energia al sistema.
Basta tuttavia un semplice esperimento per sfatare questa conclusione affrettata.
Proviamo a sciogliere del sale in acqua, il processo è ovviamente spontaneo ma se misuriamo la temperatura dell’acqua prima e dopo la dissoluzione notiamo che essa si è raffreddata.
Si tratta quindi di un processo endotermico spontaneo come possiamo spiegare questo fatto.
La spiegazione è dovuta al fatto che abbiamo trascurato di analizzare una variabile termodinamica molto importante che accompagna tutte le trasformazioni.
Questa variabile indicata con la lettera “S” è legata al disordine del sistema e prende il nome di ENTROPIA.
Un semplice esempio può essere utilizzato per associare l’entropia ad una trasformazione.
Quanta fatica dobbiamo fare per mettere in ordine una stanza e quanta per metterla in disordine?
E’ quindi una considerazione abbastanza comune che i sistemi tendano ad evolvere verso uno stato di massimo disordine spontaneamente, mentre riordinare necessita di fatica.
Un oggetto tende a rompersi e non a ripararsi spontaneamente.
Anche le reazioni chimiche e le trasformazioni fisiche seguono la logica del tendere a procedere verso un disordine è quindi verso un valore di entropia più alto di quello che avevano inizialmente.
In molti casi è facile immaginare quale sia la condizione tra due di disordine maggiore, facciamo degli esempi
- Da solido a liquido (solido particelle ordinate, liquido minori interazioni tra le particelle)
- Da liquido a gas (nel gas le particelle sono completamente libere)
- Da solido a gas (per le ragioni viste sopra)
- Reazione chimica tipo A -> B + C (reazione di decomposizione) da una molecola grande se ne ottengono tante più piccole
- etc.
Esistono quindi due parametri che determinano la spontaneità di una trasformazione:
- Un termine energetico nel nostro caso l’entalpia che favorisce le reazioni che avvengono con una sua diminuzione (reazioni esotermiche)
- Un termine legato al disordine (entropia) che favorisce le reazioni che avvengono con un suo aumento.
E’ facile prevedere come una reazione favorita sia dal punto di vista energetico (esotermica DH<0), sia del punto di vista entropico (aumento del disordine DS>0) risulti certamente spontanea.
Con analogo ragionamento possiamo prevedere che una reazione che è sfavorita sia dal punto di vista energetico (endotermica DH>0), sia del punto di vista entropico (diminuzione del disordine DS<0) risulti certamente non spontanea.
Ma cosa succede quando uno dei due termini favorisce la spontaneità, mentre l’altro la ostacola.
Nasce quindi l’esigenza di introdurre una nuova funzione di stato che tenga conto di entrambi i parametri (entalpia ed entropia) e ci dica in modo netto quando una reazione è spontanea o quando non lo è.
Questa funzione di stato prende il nome di ENERGIA LIBERA (G).
Le reazioni spontanee sono quelle che hanno una variazione di energia libera negativa (DG<0) e vengono definite esoergoniche
Le reazioni non spontanee sono quelle che hanno una variazione di energia libera positiva (DG>0) e vengono definite endoergoniche
L’espressione che consente di calcolare la variazione di energia libera è la seguente:
DG= DH-TDS
Dove T = temperatura assoluta in gradi Kelvin
°K = 273 + °C
Ricordando che la temperatura in gradi Kelvin non può assumere valori negativi (si parte dallo zero assoluto) vediamo come sia possibile applicare l’equazione di calcolo della energia libera per stabilire la spontaneità o meno di una trasformazione chimica.
Reazioni sempre spontanee (DH<0, DS>0)
supponiamo a titolo di esempio di avere questi valori
DH = -56 KJ/mole DS= +0,01 KJ/mole.°K
DG= DH – TDS = [-56 – ((T x (+0,01)]
-56 è negativo ,
(T x +0,01) sarebbe sempre positivo, ma essendoci il meno davanti sarà sempre negativo
La somma algebrica di due termini negativi darà sempre un risultato negativo indipendentemente dal valore di T
DG sarà perciò sempre negativo e quindi il processo sempre spontaneo
Reazioni sempre non spontanee (DH>0, DS<0)
supponiamo a titolo di esempio di avere questi valori
DH = +56 KJ/mole DS= -0,01 KJ/mole.°K
DG= DH – TDS = [+56 – ((T x (-0,01)]
+56 è positivo ,
(T x -0,01) sarebbe sempre negativo, ma essendoci il meno davanti sarà sempre positivo.
La somma algebrica di due termini positivi darà sempre un risultato positivo indipendentemente dal valore di T
DG sarà perciò sempre positivo e quindi il processo sempre non spontaneo.
Reazioni con DH>0 e DS>0 (segni concordi positivi)
In questo caso il processo può essere o non essere spontaneo a seconda della temperatura in cui ci troviamo a lavorare, vediamo un esempio
Analizziamo questa reazione
CaCO3 (s) –> CaO(s) + CO(g)
DH = +178 KJ/mole DS= +0,16 KJ/mole.°K
(l’aumento dell’entropia è connesso sia all’aumento del numero di molecole che alla formazione di una gas da una sostanza originalmente solida)
Se lavoriamo a temperatura ambiente (20°C = 293 °K) avremo
DG= DH – TDS = [+178 – ((293 x (+0,16)] = + 130 KJ/mole
il processo a questa temperatura non è quindi spontaneo
Ma se lavorassimo ad una temperatura di 900°C = 1173°K troveremmo
DG= DH – TDS = [+178 – ((1173 x (+0,16)] = -9,7KJ/mole
Il processo a questa temperatura diventa spontaneo
Possiamo quindi dire che le reazioni con DH>0 e DS>0 sono favorite a temperature elevate
Reazioni con DH<0 e DS<0 (segni concordi negativi)
Anche in questo caso il processo può essere o non essere spontaneo a seconda della temperatura in cui ci troviamo a lavorare, vediamo un esempio
Analizziamo la ormai conosciuta reazione
N2(g) + 3H2 (g) <-> 2NH3(g)
DH = -46 KJ/mole DS= -0,1 KJ/mole.°K
(la diminuzione dell’entropia è legata alla riduzione del numero di molecole del processo)
Se lavoriamo a temperatura ambiente (20°C = 293 °K) avremo
DG= DH – TDS = [-46 – ((293 x (-0,1)] = -16,7 KJ/mole
il processo a questa temperatura è quindi spontaneo
Ma se lavorassimo ad una temperatura di 900°C = 1173°K troveremmo
DG= DH – TDS = [-46 – ((1173 x (-0,1)] = +71,3KJ/mole
Il processo a questa temperatura diventa non spontaneo
Possiamo quindi dire che le reazioni con DH<0 e DS<0 sono favorite a temperature basse
NB: in questo caso bisogna stare attenti al discorso cinetico infatti va sempre ricordato che la temperatura rende sempre più veloci le reazioni chimiche.
Lavorare a temperatura basse può voler dire in questo caso rendere il processo spontaneo (non consumare energia per farlo avvenire), ma estremamente lento per cui spesso si devono raggiungere dei compromessi.
Energia libera ed equilibrio
Se i processi con DG>0 non sono spontanei e quelli con DG<0, invece lo sono cosa succede nei processi con DG=0?
La condizione di DG=0 corrisponde alla condizione di equilibrio termodinamico, la reazione può avvenire con la stessa probabilità in un senso o nell’altro.
Dire che una reazione ha la stessa probabilità di avvenire in un senso o nell’altro equivale a dire che la velocità della reazione diretta è uguale a quella inversa.
I concetti di equilibrio termodinamico e cinetico alla fine quindi coincidono.
Per calcolare quale sia la temperatura a cui si raggiunge un equilibrio termodinamico basta porre il DG=0, sapendo i valori di DS e DH potremo calcolare T con la seguente relazione:
T = DH/DS
(infatti: DG= DH – TDS quindi 0 = DH – TDS perciò T = DH/DS)
Ad esempio a quale temperatura la reazione
N2(g) + 3H2 (g) <-> 2NH3(g)
DH = -46 KJ/mole DS= -0,1 KJ/mole.°K
raggiunge l’equilibrio termodinamico?
T = DH/DS = -46/-0,1 = 460 °K equivalenti a 187 °C